전공/백준
2981
yha97
2022. 10. 2. 11:37
날짜 : 2022. 10. 02
사용 언어 : python
문제
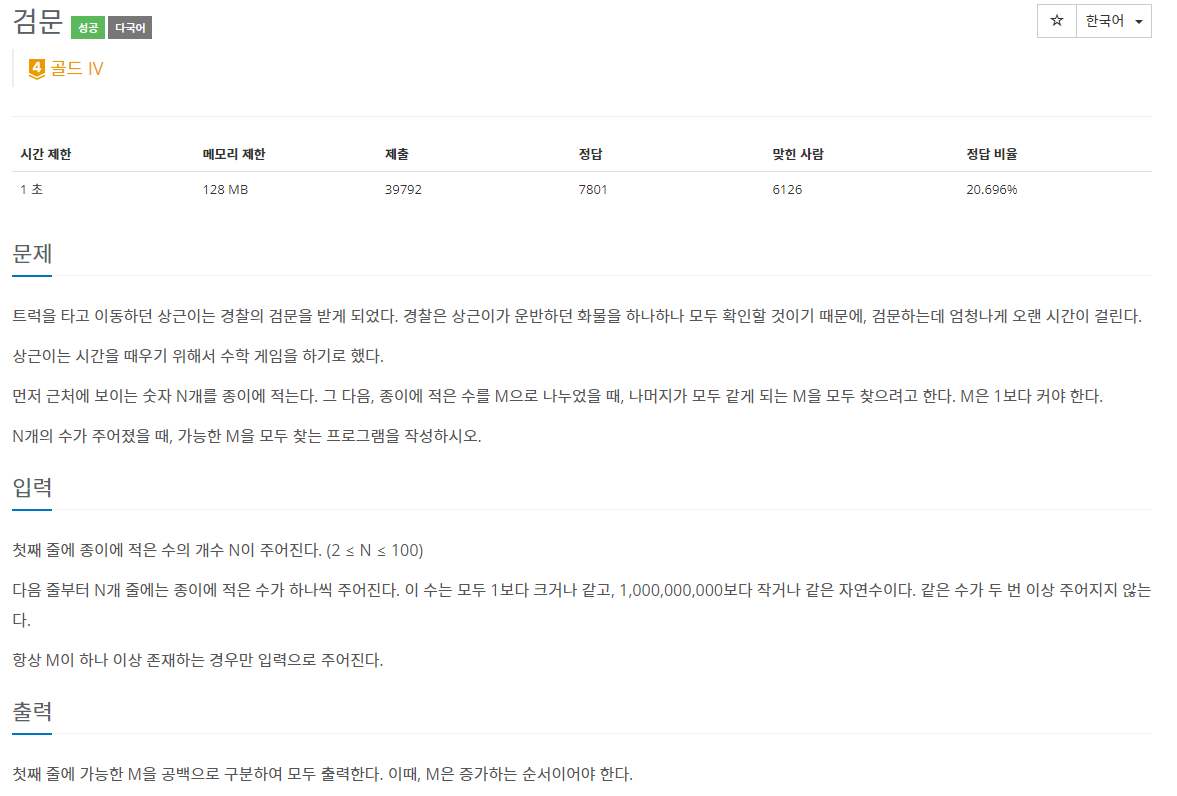

코드
import sys
import math
def gcd(a, b): # 최대공약수 구하기
if b > a : a, b = b, a
while b > 0:
tmp = b
b = a % tmp
a = tmp
return a
N = int(sys.stdin.readline()) # 테스트케이스
num = [] # 입력받은 숫자들
d = [] # 각 수들을 뺀 수의 리스트
result = []
for _ in range(N):
n = int(sys.stdin.readline()) # 숫자 입력
num.append(n)
for i in range(1, len(num)):
d.append(abs(num[i] - num[i-1]))
M = d[0] # 모든 수의 최대공약수
for i in range(1, len(d)):
M = gcd(d[i], M)
for i in range(2, int(math.sqrt(M)) + 1):
if M % i == 0:
result.append(i)
result.append(M // i)
result.append(M)
ans = list(set(result))
ans.sort()
print(*ans)
알게된 점
- 모든 수를 a * M + r 형태로 만든 다음 각 수들의 차이를 구하고 최대공약수를 구해서 풀이하는 문제다.
- 아이디어는 맞았지만 풀이과정에서 시간초과가 발생했다(약수를 구하는데 for문을 대상 숫자 전체로 돌림)
- 그래서 시간초과를 찾는데 꽤 애를 먹었고, 두 수의 차이가 1이 나오는 경우를 생각하지 못해 많은 오답이 발생했다.
- 풀이하면서 꽤나 다양한 변수를 고려해야 하는 것의 중요성을 느끼게 해 주는 문제였다.
- 그리고 gcd가 math 라이브러리로 되어있다는 것도... 잘 몰랐는데 이제야 알게 됐다
참고 사이트
- https://tmdrl5779.tistory.com/94
[백준] 2981번 (python 파이썬)
수학적 이론이 필요한 문제이다. M 을 찾아야한다. A = M * a + R B = M * b + R C = M * c + R 여기서 R을 제거하면 A - B = M ( a - b ) B - C = M ( b - c ) 이런 식이 나온다. 즉, M은 A-B, B-C의 공약수이..
tmdrl5779.tistory.com