1011

날짜 : 2023. 03. 21

사용 언어 : python

 

문제

 

 

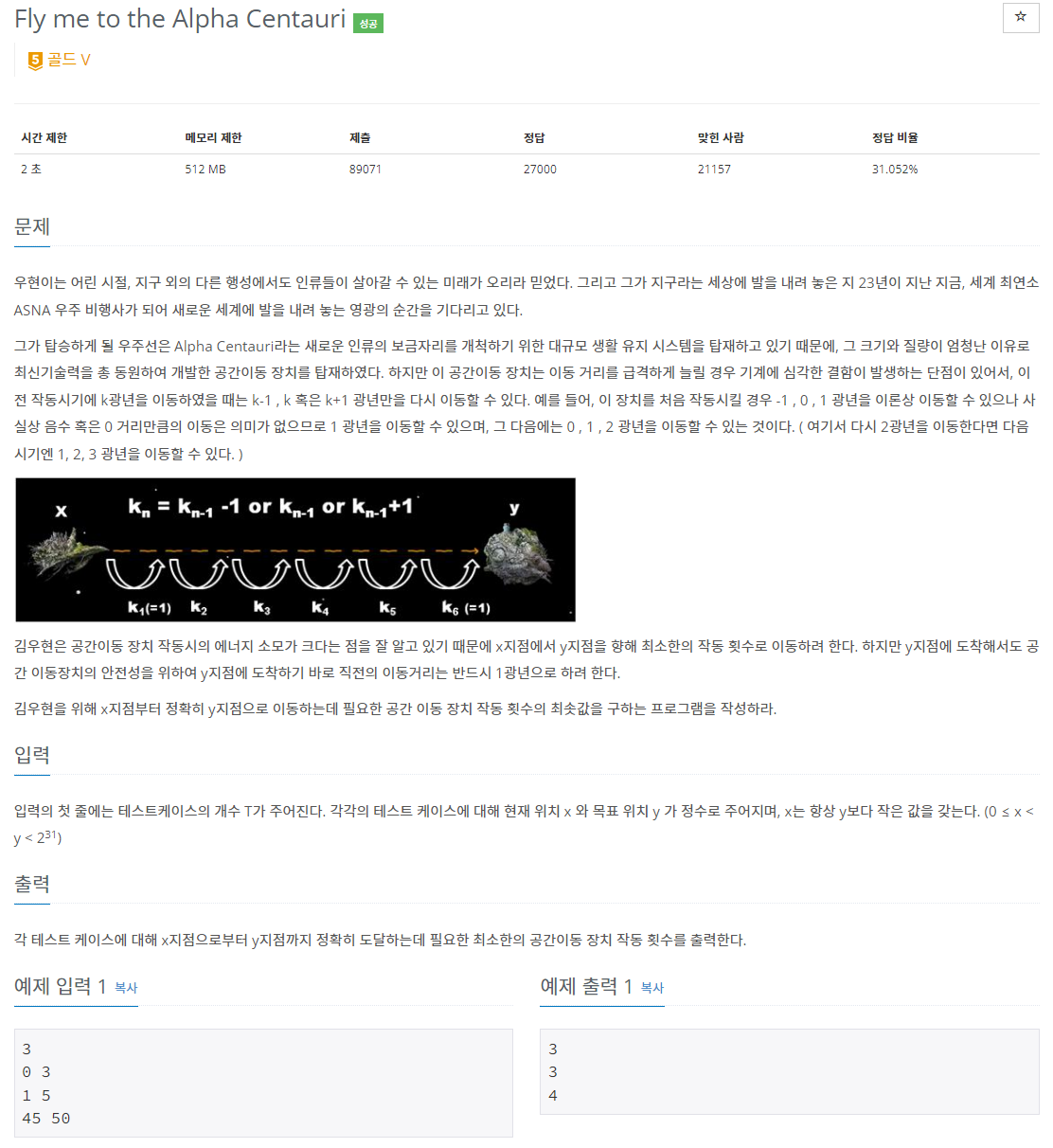
코드

import sys

t = int(sys.stdin.readline())  # 테스트케이스


def dist(l):
    n = 1
    while True:
        g = (n ** 2) - n + 1
        if l >= g:
            n += 1
        else:  # 큰 경우
            n -= 1  # 탈출
            break
    temp = l - ((n ** 2) - n + 1)
    #print(n, temp)
    if temp > (n - 1):
        res = 2 * n
    else:
        res = 2 * n - 1
    return res


for _ in range(t):
    x, y = map(int, sys.stdin.readline().split())
    d = (y - x)
    print(dist(d))

 

 

풀이

- 케이스를 하나씩 따져보았을 때, 다음과 같은 규칙이 발견된다.

1 2 3 3 4 4 5 5 5 6 6 6 7 7 7 7 8 8 8 8 ...

 

- 위의 케이스를 출몰하는 개수별로 그룹화한다면 다음과 같다.

1 2 // 3 3 4 4 // 5 5 5 6 6 6 //  7 7 7 7 8 8 8 8 ...

 

- 즉, 1과 2의 경우 1회, 3과 4의 경우 2회, 5와 6의 경우 3회 ... 이와같은 규칙성을 발견할 수 있다.

- 그러므로 이에 대해 각 그룹별 첫 번째 수의 위치에 대하여 수열을 세우면

a1 = 1, a2 = 3, a3 = 7... 과 같은 형태가 나타나고,  이를 정리하면 a[n] = n^2 - n + 1 이 도출된다.

- 다시말해 각 그룹이 바뀔 때의 위치라고 할 수 있다.

- 그 후, 그룹에 맞는 n값을 비교하면서 구하고, 나머지(거리 - a[n])를 구한 다음, 그룹에 대입하여 그 그룹에서의 숫자를 조건에 맞게 리턴하여 출력하면 된다.

 

 

알게된 점

- 고등학교 점화식을 코드로 변형하는 문제였다.

- 수학적인 공식이 있을줄 알았지만 케이스를 통해 답을 구해야 하는 문제였다.

- 19년도에는 되게 어려워서 답지를 보고 풀었는데 지금 빠르게는 아니어도 풀 수 있다는게 내심 뿌듯하다.

 

 

참고 사이트

-